Hooke's Law Explained

All there is to know from measured strain to mechanical stress

Table of content

Determination of Material Stresses from Strain Measurements
Analysis of the Biaxial Stress State with Unknown Principal Directions

Determination of Material Stresses from Strain Measurements

In the elastic deformation range of materials the methods of calculating the material stresses from the measured strains are based on Hooke's Law. In its simplest form Hooke's Law is:

σ= ε ⋅ Ε

σ= material stress [N/mm²] ε= strain [m/m] Ε= modulus of elasticity, i.e. Young’s modulus [N/mm²] This version of Hooke's Law only applies to the uniaxial stress state. Biaxial and multiaxial stress states require extended versions. Note: In strain measurements, only, the difference between an initial output condition and a condition which occurs later can be determined. The initial condition may be a load-free condition, but it may also be a condition with significant pre-loading, for example due to the object's own weight as with a bridge. Preload or also residual stress conditions can only be measured if interference with the object is allowed e.g., making a small drill hole. The material stress σ should be calculated from the measured strain ε only, according to Hooke’s Law for the uniaxial stress state as in the equation stated above, if the strain ε is measured in the active direction of the force (0° direction). In the transverse direction (90° direction), there is no material stress present despite the measurable strain (transverse contraction, transverse dilation). Therefore, for reliable results the active direction of the force must be known and the strain must be measured in this direction. If this direction is unknown or only known approximately, then the measurements and their evaluation should be carried out with the biaxial stress state in unknown principal directions. In problems in experimental stress analysis, the uniaxial stress state is more the exception rather than the rule. The biaxial stress state is met far more often, and its determination should not be undertaken with the simple method used for the uniaxial stress state; this would lead to significant errors. For a plane stress condition, the extreme normal stresses σ₁ and σ₂ occur in the perpendicular directions 1 and 2. The stresses σ₁ and σ₂ are termed the principal stresses and similarly the directions 1 and 2 are the principal directions of the stress state. If the principal normal stresses and their active directions are known, the biaxial stress condition is unambiguously defined. Known principal directions of stress are found, for example, on the surface of a round cylindrical vessel under internal pressure, on a shaft loaded with pure torsion, and in an area away from the edges, on a bent plate. With other objects and with the simultaneous action of different variables, such as normal force and bending or torsion and bending, and so forth. the principal directions must be assumed to be unknown. The principal normal stresses σ₁ and σ₂of the biaxial stress state are calculated according to the extended version of Hooke's Law from the measured principal strains ε₁ and ε₂, the material's modulus of elasticity E and Poisson's ratio v for the material:

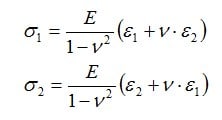It is assumed that the stress σ₃ in the principal direction 3 (perpendicular to the surface) is equal to zero. To simplify mounting procedures, X rosettes are suitable for measurements in the biaxial stress field with known principal directions. The axes of the two measuring grids must be mounted in alignment with the axes of the principal normal stresses (principal strain directions).

For objects of complex shape, with the superimposition of different types of loading (normal, bending or torsional loadings) or for points of inhomogeneity (e.g. changes in cross-sectional area), prediction of the principal directions of the stress state is generally not possible. In each case where the directions of the principal stresses are not clearly defined, the stress analysis must be carried out according to the methods described below.

Analysis of the Biaxial Stress State with Unknown Principal Directions

The principle of experimental stress analysis using strain gauges (SG) consists in using strain gauges to measure strains on the component surface. From these measured strains and the known material properties (modulus of elasticity and Poisson’s ratio), the absolute value and the direction of these mechanical stresses are determined. These calculations are based on Hooke’s Law which applies to the elastic deformation range of linear-elastic materials. In experimental stress analysis, the so-called 3-grid rosettes are used for strain measurement. These are available in versions of 0°/45°/90° and 0°/60°/120°. Both forms have a historical background. It is up to the user to choose which version to use. The 3 measuring grids of the rosettes are designated with the letters a, b and c. Therefore, a 3-grid rosette measures the three strains ε_a, ε_b and ε_c.

Measurements with 0°/45°/90° rosette

The calculation of the principal normal stresses σ₁ and σ₂ is made according to the relationship:

Measurements with the 0°/60°/120° rosette

According to this type of measuring grid arrangement of the rosette, the calculation of the principal normal stresses on σ₁ and σ₂ is made according to the equation:

The principal directions are the directions in which the principal normal stresses σ₁ and σ₂ occur as calculated using the equations above (they are identical with the principal strain directions ε₁ and ε₂). They can be determined using geometrical relationships from the strains ε_a, ε_b and ε_c measured with the R rosette. The aim of the following treatment is to provide the practical engineer with a convenient and reliable method. The theoretical aspects of Mohr's Stress Circle, which forms the basis of this treatment, are described in the specialist literature. First a tangent of an auxiliary angle ψ is calculated: For the 0°/45°/90° rosette, according to the formula

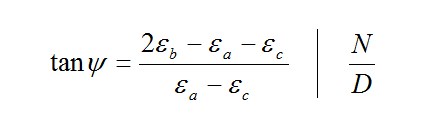For the 0°/60°/120° rosette, according to the formula

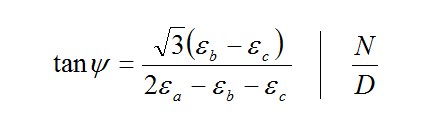Note: The tangent of an angle in the right-angled triangle is the ratio of the opposite side (numerator N) to the adjacent side (denominator D):

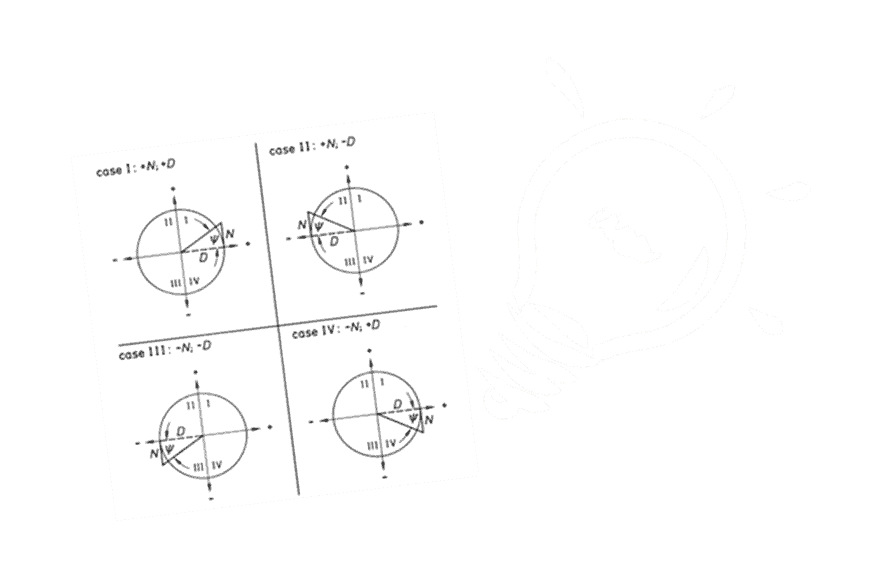
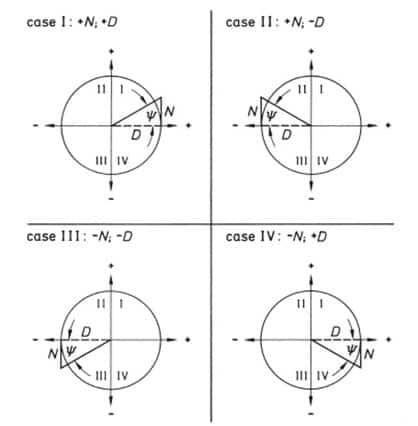
The figure below shows that the angle ψ may be in four different quadrants in the circular arc depending on the signs of the opposite and adjacent sides. null

This ambiguity of the tangent makes it necessary to determine the signs of the numerator (N) and the denominator (D) before carrying out the final calculation of the two above mentioned quotients. Determining the signs is important because they alone indicate the quadrant of the circular arc in which the angle ψ is located. From the value of the tan, the value of the intermediate angle y must first be determined

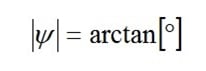Then the angle φ should be determined using the following scheme:

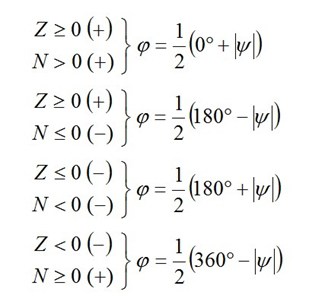The angle φ found in this manner should be applied from the axis of the reference measuring grid a in the mathematically positive direction (counter-clockwise). The axis of the measuring grid a forms one arm of the angle φ. The other arm represents the first principal direction. This is the direction of the principal normal stress σ₁ (identical with the principal strain direction ε₁). The point of the angle is located at the intersection of the axes of the measuring grids. The second principal direction (direction of the principal normal stress σ₂) has the angle φ +90°.

Support Content

No more result to load

Modern Slavery Statement Imprint Cookie Policy Privacy Policy Sitemap Ethical Business